Arifin, M. 1994. Economic injury level and sequential sampling technique for the common cutworm, Spodoptera litura (F.) on soybean. Contr. Centr. Res. Inst. Food Crops Bogor. 82: 13-37.
Muhammad Arifin
Bogor Research Institute for Food Crops
ABSTRACT
These experiments were conducted (a) to assess yield losses due to the cutworm, (b) to determine economic injury levels (EILs) for the cutworm, and (c) to develop sequential sampling techniques for the cutworm at difflrent plant growth stages of soybean. The yield losses were assessed using regression analyses of relationship between the larval population density and yield loss. The EILs were determined using the break-even point principle of the pest control, i.e., a balance between the yield loss reduction due to pest control action and cost of the pest control. The sequential sampling techniques were developed by categorizing the pest population based on their EILs. The results of the experiments indicated that soybean yield losses due to the cutworm were expressed in non-linier asymptotic regression models. The plants at late vegetative (V6-V7), blooming (R1-R2), pod formation (R3-R4), and pod filling (R5-R6) stages had the abilities to compensate leaf damages when the pest infestations were 1.9, 4.1, 3.1, and 6.8 larvae/plant, respectively. The EILs were expressed in multiple regression equations. If costs of the pest control at V6-V7, R1-R2, R3-R4, and R5-R6 stages were Rp 29,000, Rp 37,000, Rp 43,500, and Rp 43,500/ha, respectively, and the soybean price was Rp 750/kg, then the EIL values at those four plant growth stages were 1.9, 3.2, 3.2, and 6.2 for the third instar larvae/hill. Sampling activities for a control dicision making of cutworm population should be sequentially conducted in a 0.1 ha area with a minimum of seven sampling hills which were randomly selected along the diagonal lines of the field. Control decisions for the cutworm were based on the following sequential sampling models: (a) d = 1.3568 n + 8.8807 for V6-V7 stage, (b) d = 2.2314 n + 13.3157 for R1-R2 stage, (c) d = 2.2591 n + 13.4564 for R3-R4 stage, and (d) d = 4.3188 n + 23.9014 for R5-R6 stage, where d = cumulative number of larvae, n = number of samples observed, + = upper limit of the population within which a control action was necessary, and – = lower limit of the population within which a control action was not necessary.
Key words: Spodoptera litura, soybean yield loss, economic injury level, sequential sampling
INTRODUCTION
The common cutworm, Spodoptera litura (F.) is one of the most important soybean pests in Indonesia. This insect attacks leaves from vegetative to pod filling stages which may reduce the rate of photosynthesis process and cause the yield loss. At present, the control of the cutworm is still relying on insecticide which is applied at regular interval, two or more times weekly regardless the population density of the pest. This method is much insecticide consuming. Most of the insecticide application does not reach the target pest and it causes negative impacts on the environment. The recommendation for controlling the cutworm based on the Integrated Pest Management (IPM) concept has not been fully used.
According to the IPM concept, pest control is a part of the management system of an agroecosystem through integrating of all suitable pest control technologies and the natural control processes to maintain the population at a low level. The goals of IPM are: (a) reducing of pest status, (b) ensuring producer profits, (c) attaining environmental compatibility, and (d) producing sustainable solutions to pest problems (12). The use of insecticides as a control measure is justified when the benefit of the control action is equal to or exceeding the cost of the control, and when the ecosystem components are unable to control and maintain the pest population densities at a low level. Based on these basic principles of insecticide usage, the economic injury level (EIL) concept has been postulated.
The EIL is the lowest pest population density that will cause economic damage (17). It has been used to support decision making of pest control through judicious use of insecticides because at the EIL, yield loss reduction due to pest control action equals to cost of the pest control. An important component in determining the EIL is information on yield loss due to the pest. It was assumed that the yield loss of soybean due to cutworm infestation can be assessed using a non-linear regression model for relationship between the larval population density and percentage of yield loss.
Periodic monitoring using a sequential sampling technique needs to be carried out to determine when the population density of the cutworm exeeds the EIL. This would make it possible to control the cutworm population properly. There are three fundamental pieces of information neccessary for developing a sequential model, i.e., (a) mathematical distribution of the larvae, (b) EIL values, and (c) level of risks (of making a wrong decision) that the sampler is willing to accept (16).
Based on the importance of EIL values and sequential sampling techniques for controlling the cutworm, these experiments were done. The objectives were: (a) to assess yield losses due to the cutworm, (b) to determine the EILs of the cutworm, and (c) to develop sequential sampling techniques for the cutworm at different growth stages of soybean.
MATERIALS AND METHODS
Two sets of experiment were conducted, i.e., (a) EIL of the cutworm and (b) sequential sampling technique for the cutworm. These were used to make sequential sampling plans for cutworm population in the field. Soybean variety Orba was used in these experiments for host of the cutworm.
Economic Injury Level
Soybean yield loss. Two field experiments were conducted from April to July 1988 (the first dry season period) and from July to October 1988 (the second dry season period) in Pasuruan, East Java using a split-plot randomized block design with three replications. The main plots consisted of four stages of plant growth, namely V6-V7 (late vegetative), R1-R2 (blooming), R3-R4 (pod formation), and R5-R6 (pod filling) stages. The subplots consisted of five levels of larval population densities, namely 0, 4, 8, 16, and 32 larvae/eight hills (1 hill = 2 plants), respectively.
Soybean plants were grown in 5 x 5 m plots with 40 x 20 cm plant spacings. The plants consisting of eight hills/plot were covered with a 1 x 1 x 1 m nylon gauze at 11 days after sowing (das), then they were infested with different population densities of the third instar larvae at 21, 27, 40, and 55 das (10 days before treatment of main plots). Observations were conducted on the percentages of leaf damages and yields. Data were statistically processed using the analysis of variance (7). Percentages of leaf damages were measured after the larvae became prepupae, using a general formula:
∑ (ni x vi)
P = ---------------- x 100%
ZN
where P = percentage of leaf damages; ni = number of leaves with score i; vi = score i; Z = highest score (vi = 4); and N = number of leaves observed.
Score values for the leaf damages were: 0 = no damage; 1 = < 25% damage; 2 = 25-50% damage; 3 = 50-75% damage; and 4 = > 75% damage. Yield loss values for each treatment were calculated using the following formula:
Yp – Yi
Li = ------------ x 100%
Yp
where Li = percentage of yield loss at treatment i; Y = potential yield obtained at control with no treatment; and Y = actual yield at treatment i. Damage curve models and yield loss models for the cutworm were determined by comparing various regression equations (5).
EIL determination. The EILs of the cutworm were determined using the break-even point principle of the pest control, i.e., a balance between the yield loss reduction due to pest control action and cost of the pest control. The formulae was a modification of a formulae that developed by Stone and Pedigo (18) with consideration of proportional reduction in pest attack (12).
1. Gain threshold (kg/ha)
Control cost (Rp)/kg)
= ------------------------------------------------------------------
Market value (Rp/kg) x Reduction in pest attack (%)
2. % yield loss necessary
Gain threshold (kg/ha)
= -----------------------------
Potential yield (kg/ha)
3. Determination of the 6th instar larval population density necessary to cause a representative % yield loss (step 2) from a regression equation of % yield loss on larval population density.
4. Determination of the EIL for the egg masses
EIL for the 6th instar larvae (step 3)
= -------------------------------------------------------------
survival rate of the insect from eggs to
6th instar larvae (%) x number of eggs/egg mass
5. Determination of the EIL for the ith instar larvae
Survival rate of the insect from eggs to ith instar larvae
= -------------------------------------------------------------------------
Survival rate of the insect from eggs to the 6th instar larvae
x EIL for 6th instar larvae
Sequential Sampling Technique
Spatial distribution pattern. A field experiment was conducted during the 1989 dry season in Pasuruan, East Java. Soybean plants grown in a 900 m2 area were divided in to 100 plots of 2.8 x 2.8 m. Number of egg masses, young (the first and second instars) larvae, and medium (the third and fourth instars) larvae were observed randomly five hills/plot at V6-V7, R1-R2, R3-R4, and R5-R6 stages of plant growth. The data collected were used to estimate 1/k parameter which expresses a population distribution pattern, using the formula of Bliss and Owen (3). As a general rule, if 1/k < 0, the population is uniformly distributed according to the positive binomial distribution, if 1/k = 0, the population is randomly distributed according to the Poisson distribution, and if 1/k > 0, the population is aggregated in distribution according to the negative binomial distribution.
Sequential sampling model. The following parallel equations were used to develop decision lines in making the sequential sampling models (21):
d1 = bn – h1 (lower line; no treatment required)
d2 = bn + h2 (upper line; treatment required)
where d = cumulative number of larvae; b = common slope of decision line;
n = number of sampling units observed; h = intercept of decision line.
Values of b, h1 and h2 were calculated using the formulae as described by Waters (21).
Operating characteristic curve. The operating characteristic (OC) curve which provides information on the probability of a correct control decision needs to be designed to understand the work of a sequential sampling plan. The OC curve for soybean cutworm was made using the method as described by Morris (9).
Curve of average sample number. The number of samples required at different population densities of the cutworm was represented by an average sample number (ASN) curve. The ASN curve for soybean cutworm was made using the method as described by Morris (9). Efficiency of the ASN was determined by comparing the ASN and a fixed sample number (FSN).
ASN
ASN efficienrcy = (1 – ---------) x 100%
FSN
The FSN formula was derivatived by B. H. Priyanto (personal communication) based on the maximum likelihood-ratio test for the population which follow a negative binomial distribution pattern.
RESULTS AND DISCUSSION
EIL for the Cutworm
Effect of larva infestation on leaf damage and yield. Results of the experiment indicated that levels of leaf damages were increasing as the larval population density also increasing (Table 1). The highest level of leaf damage occured on plants at V6-V7 stage, followed by those on plants at R1-R2 and R3-R4 stages, while the lowest level occured on plants at R5-R6 stage. The differences in the level of leaf damages among plants at different growth stages were due to differences in leaf growth at each plant stage. The leaf growth on plants at V6-V7 and R1-R2 stages did not reach a maximum, while those at R3-R4 and R5-R6 stages did reach a maximum (19). The highest level of leaf damage occured when the leaf growth had not reached a maximum.
Soybean yields were decreased by increasing the larval population density. The infestation of one larva/two hills did not affect the yield significantly. However, the infestation of one larva/hill, affected the yield significantly (Table 2). Probably, the soybean plants still tolerated the leaf damages caused by the infestation of one larva/two hills. The level of leaf damages caused by one larva/hill on the most susceptible plant stage of V6-V7 was about 25% (Table 1). It might be that soybeans at V6-V7 to R5-R6 stages tolerated 25% of leaf damages.
Damage curve model. The general model of damage curve for the relationship between the larval population density and soybean yield of variety orba was expressed in a non-linear asymptotic equation as follow:
Y
y = --------------------------------------------------------
1 +exp (- exp [α + β exp {- √ (x + 0.1) }] )
where x = larval population density (larvae/plant); y = estimated yield; Y = potential yield;
α and β = estimated regression parameters. The estimated parameters of the regression equation models at different plant growth stages in the first and second dry season period were presented in Table 3.
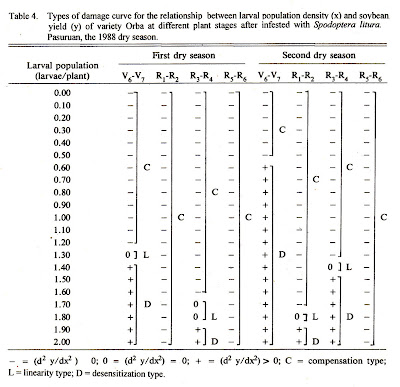
Types of the model were checked using the second derivative of the equation or d2y/dx2 as described by Priyanto et al. (15). Generally, the curves were a combination of compensation, linearity, and desensitization types (Table 4). The compensation type implied that the plant was able to prevent the injury from having its maximum effect on yield. In contrast, the linearity type represented a direct relationship between the injury level and the yield loss. The desensitization type described a diminishing yield response to the additional increments of injury (2; 13).
The soybean plants at V6-V7, R1-R2, R3-R4, and R5-R6 stages in the first dry season period could compensate the leaf damages caused by less than 1.3, 2.3, 1.7, and 3.0 larvae/plant and less than 0.6, 1.8, 1.4, and 3.8 larvae/plant in the second dry season period. On the average, the plant could compensate less than 1.9, 4.1, 3.1, and 6.8 larvae/plant (Table 4). Based on the curves, it was obvious that the ability of the plant to compensate the leaf damages at V6-V7 stage was less than at R3-R4 stage. At R3-R4 stage, it was less than at R1-R2 stage, and at R1-R2 stage, it was less than at R5-R6 stage. The low ability at V6-V7 stage indicated that the plant at this stage was most susceptible to leaf damages, whereas at R1-R2 or R3-R4 stage, the plant was able to tolerate or compensate the injury better. At R5-R6 stage, however, the plant was much less affected.
Pedigo et al. (13) mentioned that the EIL occured at or above the damage boundary which was the level of injury at which the damage occured. Because his experiment did not describe clearly the damage boundary, it was supposed that the EILs of the cutworm occured at the compensation type of the damage curve. Consequently, the linearity type of the yield loss models was not suitable for calculating the EILs. It should be based on data only from the compensation type.
Yield loss model. The yield loss models for the relationship between the larval population density and yield loss at different plant growth stages in the first and second dry season period were shown in Figure 1, while the estimated parameters of the regression equation models were presented in Table 3. The general model was expressed in a non-linear asymptotic equation:
where x = larval population density (larvae/plant); y = estimated percentage of yield loss;
α and β = estimated regression parameters; 99.99 and 0.01 = constants used to determine a suitable regression equation model. The total number of the constants was interpreted as the maximum percentage of yield loss.
EIL determination. The calculation of the EIL for the cutworm was based on the data on (a) yield loss models (Figure 1), (b) yield potential of soybean variety Orba (Table 2), (c) price/unit of yield (Rp 850/kg in the first dry season and Rp 650/kg in the second dry season), (d) cost of the pest control action (Table 5), and (e) proportional reduction in pest attack (0.8). Based on the data above and the formulae for calculating EIL, the EIL for the sixth instar larvae of the cutworm could be determined.
The EIL for the egg mass, first, second, and third instar larvae of the cutworm could be calculated based on previous experiment on (a) survival rate of the cutworm from egg mass to first, second, third, fourth, fifth, and sixth instar larvae in the soybean field, i.e., 96.1, 71.9, 45.0, 21.9, 12.7% in the first dry season and 87.0, 48.1, 25.7, 14.1, 6.7, and 3.9% in the second dry season, respectively, and (b) number of eggs/egg mass of the cutworm, i.e., 267 eggs/egg mass (1). The determination of the EILs above was less dynamic because the results were valid only for a certain situation of market price. If the market price changed, the EIL value also changed. To determine a more dynamic EIL value, it was neccessary to develop a multiple regression equation model with cost of the pest control and soybean price as variables (Table 6). This Table shows that the EIL values varied due to changes in the cost of the pest control and soybean price. The increase in pest control cost increased the EIL value, but the increase in soybean price decreased the EIL value.
Thus, if the costs of the pest control on plants at V6-V7, R1-R2, R3-R4, and R5-R6 stages were Rp 29,000, Rp 37,000, Rp 43,500, and Rp 43,500/ha, respectively and the soybean price was Rp 750/kg, the EIL values of the cutworm at those four stages were 0.021, 0.035, 0.035, and 0.071 for the egg masses/hill, 5.21, 8.47, 8.44, and 17.08 for the first instar larvae/hill, 3.35, 5.46, 5.56, and 10.82 for the second instar larvae/hill, or 1.94, 3.20, 3.24, and 6.21 for the third instar larvae/hill (Figure 2).
The recommended EIL of leaf feeding insects on soybean was 12.5% of leaf damage (4). This value was obtained from the experiment on soybean yield loss caused by different levels of artificial defoliation (20). An assessment of yield loss using artificial defoliation method was followed by the authors because it is easy to use. However, it is not very reliable method because it does not express the dynamic process of defoliation by leaf feeders and the natural plant ability to compensate the leaf damages (6; 10).
In these experiments, EIL of soybean cutworm was determined by the insect infestation method. According to Hammond and Pedigo (8), this method was more reliable than the artificial defoliation method. Therefore, the EIL of the cutworm determined in these experiments should be suitable for a guidance in control decision making for the soybean cutworm.
Sequential Sampling Technique
Spatial distribution pattern. Results of the experiment indicated that the mean number of egg mass populations was equal to the variance, with 1/k distribution parameter almost zero, whereas those of the young and medium instar larvae were lower than the variance with 1/k value higher (Table 7). Based on 1/k parameter, the population of egg masses was randomly distributed according to the Poisson distribution. Possibly, every plant unit had an equal probability of being occupied by an egg mass. The population of young and medium instar larvae was aggregated in distribution according to the negative binomial distribution. The presence of an individual larva at a plant unit might increase the probability of other larva to come nearby.
There was a trend that an individual larva was randomly distributed when the mean population and the variance were relatively low, and it was aggregated in distribution when the mean and the variance were relatively high. The larva distribution was not significantly different at each plant growth stage. Therefore, the distribution pattern of the larva was affected by the stage, population density, and variance of the insects.
Correlation analysis of sample mean to 1/k value for the young instar larvae was significant (r= 0.9941**), while that of the medium instar larvae was not significant (r= 0.4435ns). Bliss and Owen (3) indicated that when the correlation was not significant, the calculation of a common value for 1/k (1/kc) was neccessary. Based on the method, 1/kc value for the medium instar larvae was 2.5356 or within the range from 1.5138 to 3.5139.
A sampling method with highly precision and efficiency could be determined based on the distribution pattern of the cutworm. Results of the previous experiment indicated that when the population was randomly distributed, the suitable sampling method was simple random. Whereas, when the population was aggregated in distribution, the sampling method was random along the diagonal lines of the field (11;14). In this case, the suitable sampling method for the egg mass was simple random, while the method for young and medium instar larvae was random along the diagonal lines of the field.
Sequential sampling plan. The sequential sampling plans for the third instar larvae of the cutworm at different plant growth stages of soybean variety orba were shown in Figures 3 and Table 8. To determine these plans, the risk level of the pest control decision was set at α = β = 0.20 and the population levels below which treatments would not be required were set at 1/2 of the ElL.
The minimum numbers of samples observed on plants at V6-V7, R1-R2, R3-R4, and R5-R6 stages were 7, 6, 6, and 6 sampling units, respectively. When the accumulated number of larvae was above or below the decision lines, the sampling was stopped and a decision was made, whether to control or not. When the accumulative number of larvae was between the lower and the upper limits of the decision lines, a decision could not be made, and the field would be sampled using the same procedure 3-4 days later.
Operating characteristic curve. The probability of making correct decision for controlling the third instar larvae of soybean cutworm at various population densities was indicated by the operating characteristic curves (Figure 4). Based on the risk level of wrong decision making (β) = 0.2, the larva population for probability of 80% correct control decision on plants at V6-V7, R1-R2, R3-R4, and R5-R6 stages were 1.9, 3.2, 3.2, and 6.2 larvae/hill, respectively. When the larva population was higher, the risk level (β) was less than 0.2 and the probability of making a correct decision was more than 80%.
Curve of average sample number. The average number of samples to be observed for controlling the third instar larvae of soybean cutwonn at different population densities was indicated by ASN curves (Figure 5). These gave the average expected number of samples required for making a control decision at any level of population. The ascending portion of the curves indicated that a control decision was not neccessary, whereas the descending portion of the curves indicated that a control decision was necessary. Based on the curves, the average number of samples for making control decisions at V6-V7, R1-R2, R3-R4, and R5-R6 stages were 9, 8, 8, and 8 sampling units. These were observed at the population densities of 1.9, 3.2, 3.2, and 6.2 larvae/hill, respectively. A less number of sampling units were observed when the larval population densities were higher. At the same value with the EIL and level of risk, sampling with the ASN was 58% more efficient than the FSN, and was 45% more efficient than the method recommended by the Directorat of Plant Protection (DPP) (4) (Table 9).
Population monitoring. A monitoring activity for cutworm population should be sequentially conducted in a 0.1 ha area by direct counting of the population from a minimum of seven sampling hills which were randomly selected along the diagonal lines of the field. Observations of cutworm population included stages of egg masses, first, second, and third instar larvae. The population of the first instar larvae was not dispersed while the second instar larvae started to disperse. Therefore, to make the calculation easy, it was assumed that a group of the first instar larvae was equal to an egg mass, the second instar larvae was equal to the third instar larvae, and one egg mass or one group of the first instar larvae was equal to 95 larvae of the third instar (1).
Data collected from the sampling activities were fitted to the sequential sampling model for a plant growth stage. There were three categories for control decision making, namely:
A: If the accumulated number of larvae was below the lower limit of the decision lines, it was decided that a control action was not neccessary. The next sampling would be conducted a week later.
B: If the accumulated number of larvae was above the upper limit of the decision lines, it was decided that a control action was neccessary. Next sampling would be conducted 2 weeks later.
C: If the accumulated number of larvae was between the lower and the upper limits of the decision lines, the sampling activity was stopped and the next sampling would be conducted 3-4 days later. After this, if the accumulated number of larvae was still between the lower and the upper limits or below the lower limit of the decision lines, a control action was not neccessary, but if it was above the upper limit, a control action was neccessary.
The sequential sampling models for the cutworm above was relatively accurate because they could tolerate a risk level of wrong decision at (β)= 0.2. Besides, the models were simple and easy to implement for monitoring activities and to make control decisions for the cutworm in the field. This guidance was better than the previous guidance which was based on an empirical pest population densities or leaf damage levels, thus it was suitable to be used in the IPM program.
CONCLUSIONS
Based on the results of the experiments on the EIL and sequential sampling technique for the cutworm on soybean variety orba which were conducted during 1988 to 1989 in Pasuruan, it was concluded that:
1. The EIL values of the cutworm at different control costs and soybean prices were determined by a multiple regression equation model. If the cost of the pest control on plants at V7-V8, R1-R2, R3-R4, and R5-R6 stages were Rp 29,000, Rp 37,000, Rp 43,500/ha, respectively and the soybean price was Rp 750/kg, the EIL values of the cutwom at those four plant growth stages were 0.021, 0.035, 0.035, and 0.071 for the egg masses/hill, 5.21, 8.17, 8.44, and 17.08 for the first instar larvae/hill, 3.35, 5.46, 5.56, and 10.82 for the second instar larvae/hill, or 1.94, 3.20, 3.24, and 6.21 for the third instar larvae/hill.
2. Soybean yield losses due to the cutworm at different plant growth stages could be assessed by a non-linear asymptotic model. The highest level of the yield loss occured on plants at V6-V7 stage, followed by those at R3-R4, R1-R2, and R5-R6 stages, respectively.
3. The relationship between the larval population density and yield at different plant growth stages were expressed in a non-linear asymptotic model of damage curve. The curves were a combination of compensation, linearity, and desensitization types. The plants at V6-V7, R1-R2, R3-R4, and R5-R6 stages could compensate the leaf damages caused by less than 1.9, 4.1, 3.1, and 6,8 larvae/plant, respectively.
4. Monitoring activities for cutworm population should be sequentially conducted in a 0.1 ha area from a minimum of seven sampling hills which were randomly selected along the diagonal lines of the field. Control decisions for the cutworm were based on the following sequential sampling models: (a) d = 1.3568 n ± 8.8807 for V6-V7 stage, (b) d = 2.2314 n ± 13.3157 for R1-R2 stage, (c) d = 2.2591 n ± 13.4564 for R3-R4 stage, and (d) d = 4.3188 n ± 23.9014 for R5-R6 stage, where d = cumulative number of larvae, n = number of samples observed, + = upper limit of the population within which a control action was neccessary, and – = lower limit of the population within which a control action was not neccessary.
5. The monitoring method based on EIL values and sequential sampling models for cutworm population was suitable for the IPM program on soybean because it was simple, practical, and relatively accurate with a risk level of wrong decision β = 0.2. The method should be developed further considering existence and abundance of natural enemies in the field.
ACKNOWLEDGEMENTS
The author wishes to express his gratitude to Dr. Ida Nyoman Oka, Dr. Kasumbogo Untung, and Dr. Soeprapto Mangoendihardjo for their encouragements. He also wishes to thank Ir. Budi Hari Priyanto for his exellent guidance and help.
RINGKASAN
Tingkat Kerusakan Ekonomi dan Teknik Penarikan Contoh Populasi Ulat Grayak, Spodoptera litura (F.) pada Tanaman Kedelai.
Dua set percobaan telah dilakukan pada tahun 1988-1989 di Pasuruan dengan tujuan (a) menduga kehilangan hasil panen akibat infestasi ulat grayak, (b) menentukan tingkat kerusakan ekonomi (TKE) ulat grayak, dan (c) mengembangkan teknik penarikan contoh beruntun populasi ulat grayak pada berbagai stadia tanaman kedelai. Kehilangan hasil panen akibat infestasi ulat grayak diduga dengan menganalisis hubungan antara kepadatan populasi ulat dan kehilangan hasil panen. Nilai TKE ulat grayak ditentukan dengan menerapkan prinsip impas pengendalian hama yakni kesetaraan antara nilai kehilangan hasil yang diselamatkan oleh tindakan pengendalian hama dan biaya pengendalian hama. Teknik penarikan contoh beruntun ulat grayak dikembangkan dengan mengkategorikan populasi hama berdasarkan nilai TKE.
Hasil penelitian menunjukkan bahwa kehilangan hasil panen kedelai akibat infestasi ulat grayak dinyatakan dengan model regresi yang bersifat nonlinier asimptotik. Tanaman pada stadia V6-V7, R1-R2, R3-R4, dan R5-R6 mampu mengkompensasi kerusakan daun apabila diinfestasi ulat, masing-masing kurang dari 1,9; 4,1; 3,1; dan 6,8 ekor/tanaman. Nilai TKE ulat grayak dinyatakan dengan model regresi berganda. Apabila biaya pengendalian pada stadia V6-V7, R1-R2, R3-R4, dan R5-R6, masing-masing Rp 29.000, Rp 37.000, Rp 43.500, dan Rp 43.500/ha dan harga kedelai Rp 750/kg, maka TKE pada keempat stadia tersebut, masing-masing 1,9, 3,2, 3,2, dan 6,2 ekor ulat instar III/rumpun.
Penarikan contoh untuk keputusan pengendalian ulat grayak dianjurkan untuk dilakukan secara beruntun pada tiap lahan seluas 0,1 ha dengan minimum tujuh rumpun contoh yang ditentukan secara acak berdasarkan garis diagonal lahan. Model keputusan pengendalian yang digunakan adalah sebagai berikut: (a) d = 1,3568 n ± 8,8807 untuk stadia V6-V7, (b) d = 2,2314 n ± 13,3157 untuk stadia R1-R2, (c) d = 2,2591 n ± 13,4564 untuk stadia R3-R4, dan (d) d = 4,3188 n ± 23,9014 untuk stadia R5-R6, dimana d = banyaknya ulat kumulatif, n = banyaknya contoh yang diperiksa + = batas bahaya populasi yang harus segera dikendalikan, dan – = batas aman populasi yang tidak perlu dikendalikan.
REFERENCES
1. ARIFIN, M. 1993. Ambang ekonomi dan teknik pengambilan contoh populasi ulat grayak, Spodoptera litura (F.) pada tanaman kedelai. Disertasi Universitas Gadjah Mada, Yogyakarta.
2. BARDNER, R., and K.E. FLETCHER. 1974. Insect infesations and their effects on the growth and yield of field crops: A review. Bull. Ent. Res. 64: 141-60.
3. BLISS, C.I., and A.R.G. OWEN. 1958. Negative binomial distribution with a common k. Biometrika 45: 37-58.
4. DITLINTAN. 1989. Pedoman pengamatan dan pelaporan perlindungan tanaman pangan. Ditlintan, Jakarta.
5. DRAPER, H., and H. SMITH. 1981. Applied linier regression analysis. John Wiley & Sons, New York.
6. FERRO, D.N., B.J. MORZUCH, and D. MARGOLIES. 1983. Crop loss assessment of the Colorado potato beetle (Coleoptera: Chrysomelidae) on potatoes in Western Massachusetts. J. Econ. Entomol. 76: 349-56.
7. GOMEZ, K.A., and A.A. GOMEZ. 1984. Statistical procedures for agricultural research, 2nd ed. John Wiley & Sons, New York.
8. HAMMOND, R.B, and L.P. PEDIGO. 1976. Sequential sampling plans for the green cloverworm in Iowa soybeans. J. Econ. Entomol. 69: 181-5.
9. MORRIS, R.F. 1954. A sequential sampling technique for spruce budworm egg surveys. Can. J. Zool. 33: 302-13.
10. NEWSOM, L.D., M. KOGAN, F.D. MINER, R.L. RABB, S.C. TURNIPSEED, and W.H. WHITCOMB. 1980. General accomplishments toward better pest control in soybean, p. 51-97. In C.B. Huffaker (ed.). New technology of pest control. John Wiley and Sons, New York.
11. NISHIDA, T., and T. TORII. 1970. A handbook of the field methods for research on rice stem borers and their natural enemies. Burgass and Sons (Abingdon). IBP Handbook no. 14.
12. PEDIGO, L.P., and L.G. HIGLEY. 1992. The economic injury level concept and environmental quality. American Entomologist 38(1): 12-21.
13. PEDIGO, L., S.H. HUTCHINS, and L.G. HIGLEY. 1986. Economic injury levels in theory and practice. Ann. Rev. Entomol. 31: 341-68.
14. PIETERS, E.P., and W.L. STERLING. 1974. A sequential sampling plan for the cotton fleahopper, Pseudatomoscelis seriatus. Environ. Entomol. 3: 102-6.
15. PRIYANTO, B.H., J. SOEJITNO, H. TJATUR, dan WALUYO. 1992. Ambang ekonomi penggerek batang padi putih, Scirpophoga innotata (Walker). Prosiding Hasil Penelitian Pendukung PHT, Program Nasional PHT, Bappenas. Cisarua, 7-8 September 1992.
16. SHEPARD, B.M. 1980. Sequential sampling plans for soybean arthropods, p. 79-93. In M. Kogan and D.C. Herzog (eds.). Sampling methods in soybean entomology. Springer-Verlag, New York.
17. STERN, V.M., R.F. SMITH, R.van den BOSCH, and K.S. HAGEN. 1959. The inregrated control concept. Hilgardia 29: 81-101.
18. STONE, J.D., and L.P. PEDIGO. 1972. Development and economic injury level of the green cloverworm on soybean in Iowa. J. Econ. Entomol. 65: 197-201.
19. TAKAGI, H., and S. SUMADI. 1984. Growth of soybean as affected by plant density. Penelitian Pertanian 4(2): 83-6.
20. TENGKANO, W., and T. SUTARNO. 1982. Influence of leaf attact at generative stage on yield of Orba soybean variety. Penelitian Pertanian 2: 51-3.
21. WATERS, W.E. 1954. Sequential sampling in forest insect surveys. For. Sci. 1: 68-79.













Tidak ada komentar:
Posting Komentar